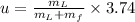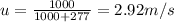Question

A lumberjack (mass = 103 kg) is standing at rest on one end of a floating log (mass = 277 kg) that is also at rest. The lumberjack runs to the other end of the log, attaining a velocity of +3.74 m/s relative to the shore, and then hops onto an identical floating log that is initially at rest. Neglect any friction and resistance between the logs and the water. (a) What is the velocity of the first log (again relative to the shore) just before the lumberjack jumps off? (b) Determine the velocity of the second log (again relative to the shore) if the lumberjack comes to rest relative to the second log.

Answer 1

Step-by-step explanation:

Given

mass of lumber jack
`m_L=1000 kg`

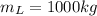
mass of floating log
`m_f=277 kg`

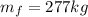
velocity of lumber jack =3.74 m/s (w.r.t. shore)

conserving momentum

Initial momentum=Final momentum

`0=m_L* 3.74+m_f* v`

`v=-(1000* 3.74)/(277)`

`v=-13.501 m/s`

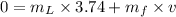
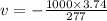
(b)For second Log

Conserving Momentum

Initial momentum of log and Lumber jack=Final momentum of log and lumberjack

`m_L* 3.74=(m_L+m_f)u`

u is final velocity of lumberjack and log

`u=(m_L)/(m_L+m_f)* 3.74`

`u=(1000)/(1000+277)=2.92 m/s`