Question

Robert took $32 with him to spend on pizza and games for himself and his friends at Chucky Cheese. The price for each slice of pizza was $4. The price for each game was half the price of a slice of pizza.

a) Sketch the graph that represents the situation and label the intercepts with the real world items you are comparing. Use one axis to represent the number of slices of pizza and the other axis to represent the number of games.
b) What do the intercepts and the solutions of your graphed function mean in context of the problem? Explain both intercepts.
c) If Robert spends his money on both pizza and games, give an example of the number of pizza slices and games Robert can buy if he spends all his money.
d) Prove algebraically that you’re above example in C is true.

Answer 1

Part a) The graph in the attached figure

Part b) see the explanation

Part c) 6 slices of pizza and 4 games

Part d) see the explanation

Explanation:

Part a)

Let

x ----> the number of slices of pizza

y ---> the number of games

we know that

The price for each slice of pizza was $4

The price for each game was half the price of a slice of pizza

so

$4(1/2)=$2 ----> the price of each game

The number of slices of pizza multiplied by $4 plus the number of games multiplied by $2 must be equal to $32

so

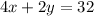`4x+2y=32` -----> equation A

using a graphing tool

see the attached figure

The x-intercept is the point (8,0)

The y-intercept is the point (0,16)

Part b) What do the intercepts and the solutions of your graphed function mean in context of the problem

The y-intercept -----> that means, the value of y when the value of x is equal to zero

so

In this context, if they spend all money on games, they can play 16 games

The x-intercept -----> that means, the value of x when the value of y is equal to zero

so

In this context, if they spend all money on slices of pizza, they can buy 8 slices of pizza

Part c) we know that

If a ordered pair is a solution of the liner equation , then the ordered pair must satisfy the linear equation

Example

The ordered pair (6,4) lie on the line

Verify

For x=6 slices of pizza, y=4 games

substitute

`4(6)+2(4)=32`

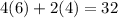
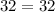`32=32` ---> is true

Part d)

x-intercept

For y=0

Find the value of x

`4x+2(0)=32`

`4x=32`

`x=8`

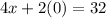
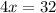
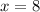
The x-intercept is the point (8,0)

8 slices of pizza and 0 games

y-intercept

For x=0

`4(0)+2y=32`

`2y=32`

`y=16`

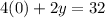
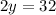
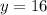
The y-intercept is the point (0,16)

0 slices of pizza and 16 games