Answers:
a)
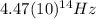
b)
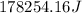
c)
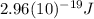
Explanation:
a) The following equation states the relation between the wavelength
 and the frequency
and the frequency
 of the light:
of the light:
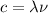 (1)
(1)
Where:
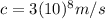 is the speed of light in vacuum
is the speed of light in vacuum
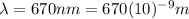 is the wavelength of the light emitted by the laser pointer
is the wavelength of the light emitted by the laser pointer
 is the frequency
is the frequency
Finding
 :
:
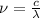 (2)
(2)
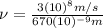 (3)
(3)
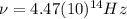 (4) This is the frequency
(4) This is the frequency
b) The energy
 of a 670 nm photon is given by:
of a 670 nm photon is given by:
 (5)
(5)
Where:
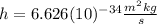 is the Planck constant
is the Planck constant
Then:
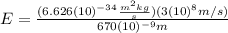 (6)
(6)
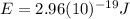 (7) This is the energy of one photon
(7) This is the energy of one photon
Now we have to find the energy of 1 mole of these 670 nm photons by multiplying (7) by the Avogadro's number (
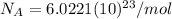 ):
):
 (8)
(8)
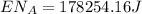 This is the energy of 1 mole of 670 nm photons
This is the energy of 1 mole of 670 nm photons
c) The ground state of an atom is the point where the energy of the system is zero. This means the ground state energy is
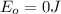 and the energy gap
and the energy gap
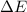 is:
is:
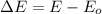
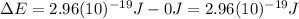
Hence, the energy gap has the same value that was already calculated in part b (7), which is the energy of 670 nm photons:
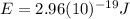
This is the energy of a single 670 nm photon, which is emitted when the excited electrons return to the ground state.
That is why the wavelength (color) of the light of the laser pointer is 670 nm (red).