Question

What is the completely factored form of d^4 - 81

Answer 1

(d - 3)(d + 3)(d² + 9)

Explanation:

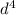`d^(4)` - 81 ← can be factored as a difference of squares

a² - b² = (a - b)(a + b), thus

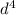`d^(4)` - 81

= (d²)² - 9²

= (d² - 9)(d² + 9)

Note that d² - 9 is also a difference of square, so

= (d - 3)(d + 3)(d² + 9) ← in factored form

Answer 2

Explanation:

d^4-81

(d^2)^2-(9)^2

Using formula

(d^2+9)(d^2-9)