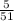Question

There are 12 brown socks and 6 blue socks in a drawer. In the dark, Jason pulls out a sock and puts it on his right foot. Then he pulls out another sock and puts it on his left foot.

What is the probability that Jason has two blue socks on his feet?

Answer 1

The probability that Jason has blue socks is
`(5)/(51)`

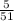
Solution:

Given, there are 12 brown socks and 6 blue socks in a drawer.

So, total number socks = 12 + 6 = 18 socks

In the dark, Jason pulls out a sock and puts it on his right foot.

Now, let the probability of pulled sock to be blue sock

`=\frac{\text {number of blue socks}}{\text {total number of socks}}=(6)/(18)=(1)/(3)`

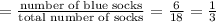
Then, available socks = 18 – 1 picked sock = 17 socks and number of blue socks = 6 – 1 = 5

Then he pulls out another sock and puts it on his left foot

Now, the probability that second picked sock will also be blue =
`\text { probability of } 1 \text { sock } * \frac{\text { blue socks count }}{\text { socks count }}`

`=(1)/(3) * (5)/(17)=(5)/(51)`

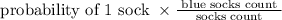
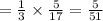
Hence, the probability that Jason has blue socks is
`(5)/(51)`