Question

Thompson and Thompson is a steel bolts manufacturing company. Their current steel bolts have a mean diameter of 142 millimeters, and a standard deviation of 6 millimeters. If a random sample of 35 steel bolts is selected, what is the probability that the sample mean would be greater than 139.7 millimeters? Round your answer to four decimal places.

Answer 1

Answer: 0.9884

Explanation:

Given : Population mean :
`\mu=142`

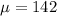
and standard deviation :
`\sigma=6`

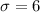
sample size : n= 35

Let x be the random variable that represents the diameter of steel bolts.

Using formula
`z=(x-\mu)/((\sigma)/(√(n)))` ,

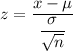The z-value corresponds to x=139.7

`z=(139.7-142)/((6)/(√(35)))\approx-2.27`

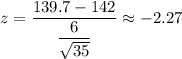
The probability that the sample mean would be greater than 139.7 millimeters will be :-

`P(x>139.7)=P(z>-2.27)=1-P(z<-2.27)\\\\=1-(1-P(z<2.27))=P(z<2.27)\\\\=0.9883962\approx0.9884`

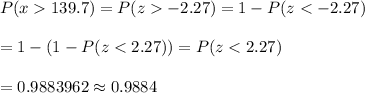
Hence, the required probability : = 0.9884