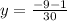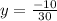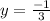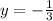Answer:
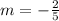 ---- slope
---- slope
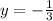 --- y intercept
--- y intercept
Explanation:
Given
The attached table
Required
Calculate the slope and y intercept
First, we need to calculate the slope
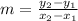
From the table, the following relationships exist:
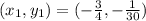
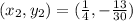
So, the expression for calculating slope becomes:
![m = [-(13)/(30) - (-(1)/(30))] / [(1)/(4) - (-(3)/(4))]](https://img.qammunity.org/2022/formulas/mathematics/college/gzmqc8v2jql0ubdi3xw446vfb4jt89b8yd.png)
![m = [-(13)/(30) +(1)/(30)] / [(1)/(4) +(3)/(4)]](https://img.qammunity.org/2022/formulas/mathematics/college/wpbaebhkdcctoc8w8jkjl0pk0jmni3u51f.png)
Take LCM
![m = [(-13+1)/(30)] / [(1+3)/(4)]](https://img.qammunity.org/2022/formulas/mathematics/college/6q1okni7zr38zsblqogh7jov9vzwhxoddi.png)
![m = [(-12)/(30)] / [(4)/(4)]](https://img.qammunity.org/2022/formulas/mathematics/college/znhednijz0b68yfqw7s20rvb27wnlzpkii.png)
![m = [(-12)/(30)] / 1](https://img.qammunity.org/2022/formulas/mathematics/college/3yw9i25wrovdyw7dnqvnduarpeiudsbdd4.png)
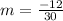
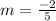
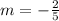
To calculate the y intercept:
x must be 0. i.e.
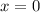
So, we have:
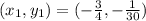
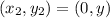
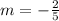
Substitute these values in:
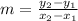
![-(2)/(5) = [y - (-(1)/(30))] / [0- (-(3)/(4))]](https://img.qammunity.org/2022/formulas/mathematics/college/7oeyxnh3nsf41glmth5v9j7t5sx3spirhl.png)
![-(2)/(5) = [y +(1)/(30)] / [0+(3)/(4)]](https://img.qammunity.org/2022/formulas/mathematics/college/39ajdeofmzcatybnk1zlq1ap65a5ss1z6r.png)
![-(2)/(5) = [y +(1)/(30)] / [(3)/(4)]](https://img.qammunity.org/2022/formulas/mathematics/college/wszxvp6sw6v7ob6n059w95rnx3afvb3tm7.png)
Multiply through by 3/4
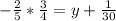
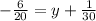
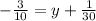
Collect Like Terms