The domain of the relation is
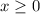 , representing time in minutes, and the range is
, representing time in minutes, and the range is
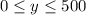 , representing the amount of water drained from the heater in gallons.
, representing the amount of water drained from the heater in gallons.
Let's analyze the given coordinates and determine the domain and range of the relation:
Coordinates: (0,500), (20,400), (40,200), (50,200), (20,0)
**Domain:** The x-coordinates represent time (in minutes), and they start at 0 and increase. Therefore, the domain is
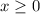 .
.
**Range:** The y-coordinates represent the amount of water drained from the heater (in gallons), and they decrease as draining occurs. The lowest value is 0, and the highest value is 500. Therefore, the range is
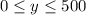 .
.
So, the correct choices are:
B.
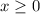
A.
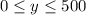
Therefore, the correct answer is the combination of B and A.