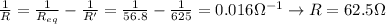Question

A 100 W, 250 V lamp is connected in parallel with a resistance R across a supply voltage of 250 V. The total power in the circuit is 1100 W. Find the value of R

Answer 1

`62.5 \Omega`

Step-by-step explanation:

First of all, we calculate the resistance of the lamp. The power of the lamp is given by

`P=(V^2)/(R')`

Where

P = 100 W is the power

V = 250 V is the voltage

R' is the resistance of the lamp

Solving for R',

`R'=(V^2)/(P)=(250^2)/(100)=625 \Omega`

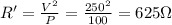
Now this resistance is connected in parallel to the other resistance R, so their equivalent resistance is

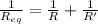`(1)/(R_(eq))=(1)/(R)+(1)/(R')` (1)

Now the total power in the circuit is

P = 1100 W

And the voltage is

V = 250 V

So we can write

`P=(V^2)/(R_(eq))`

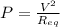
to find the equivalent resistance:

`R_(eq)=(V^2)/(P)=(250^2)/(1100)=56.8 \Omega`

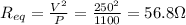
Therefore, rearranging (1), we find R:

`(1)/(R)=(1)/(R_(eq))-(1)/(R')=(1)/(56.8)-(1)/(625)=0.016 \Omega^(-1) \rightarrow R=62.5 \Omega`