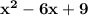Answer:
1) Solving the term
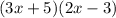 using F.O.I.L we get
using F.O.I.L we get
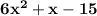
2) solving the term
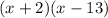 using F.O.I.L we get
using F.O.I.L we get
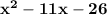
3) Solving
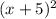 using square of binomial we get
using square of binomial we get
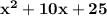
4) Solving
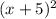 using square of binomial we get
using square of binomial we get
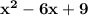
Explanation:
1) (3x + 5)(2x - 3). Solve using the F.O.I.L.
F.O.I.L stands for First, Outer Inner Last
We have
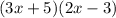
First: 3x(2x)
Outer: 3x(-3)
Inner: 5(2x)
Last: 5(-3)
Solving we get:
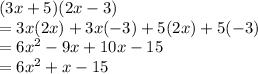
So, solving the term
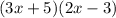 using F.O.I.L we get
using F.O.I.L we get
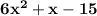
2) (x + 2)(x – 13). Solve using the F.O.I.L.
F.O.I.L stands for First, Outer Inner Last
We have
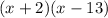
First: x(x)
Outer: x(-13)
Inner: 2(x)
Last: 2(-13)
Solving we get:
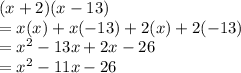
So, solving the term
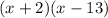 using F.O.I.L we get
using F.O.I.L we get
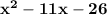
3) (x + 5)^2. Solve using the square of Binomial.
The square of binomial is:
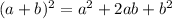
Solving:
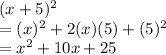
So, solving
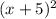 using square of binomial we get
using square of binomial we get
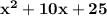
4) (x -3)^2. Solve using the square of Binomial.
The square of binomial used is:
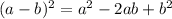
Solving:
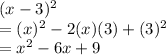
So, solving
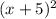 using square of binomial we get
using square of binomial we get