Question

Lotteries are an important income source for various governments around the world. However, the availability of lotteries and other forms of gambling have created a social problem: gambling addicts. A critic of government-controlled gambling contends that 30% tickets are gambling addicts. If we randomly select 10 people among those who report that they regularly buy lottery tickets, What is the probability that more than 5 of them are addicts?

Answer 1

Answer: 0.0473

Explanation:

Given : The proportion of gambling addicts : p=0.30

Let x be the binomial variable that represents the number of persons are gambling addicts.

with parameter p=0.30 , n= 10

Using Binomial formula ,

`P(x)=^nC_xp^x(1-p)^(n-x)`

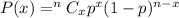
The required probability =
`P(x>5)=P(6)+P(7)+P(8)+P(9)+P(10)\\\\=^(10)C_6(0.3)^6(0.7)^(4)+^(10)C_7(0.3)^7(0.7)^(3)+^(10)C_8(0.3)^8(0.7)^(2)+^(10)C_9(0.3)^9(0.7)^(1)+^(10)C_(10)(0.3)^(10)(0.7)^(0)\\\\=(10!)/(4!6!)(0.3)^6(0.7)^(4)+(10!)/(3!7!)(0.3)^7(0.7)^(3)+(10!)/(2!8!)(0.3)^8(0.7)^(2)+(10!)/(9!1!)(0.3)^9(0.7)^(1)+(1)(0.3)^(10)\\\\=0.0473489874\approx0.0473`

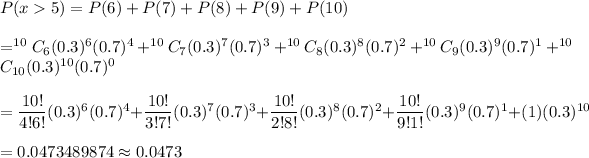
Hence, the required probability = 0.0473