Answer:
A) The initial height is 32
B) The higher height that the ball gets is 68
C) at
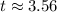
Explanation:
A) For this part you only have to evaluate the function in t=0, this is:
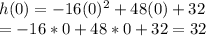
B) To obtain the higher height you have to find the maximum value that reaches the function
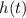 . For this we can use the first derivative rule.
. For this we can use the first derivative rule.
Then we have:
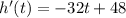
How we only have one extreme point we assume that this is a maximum, and this point is in the value
![t\[tex] such that [tex]h'(t)=0](https://img.qammunity.org/2020/formulas/mathematics/high-school/ca6pmryhx20ff5n4dgokcewl5svovj6toa.png) , this is
, this is
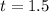 . Then, evaluate the function
. Then, evaluate the function
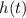 in
in
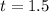
we have
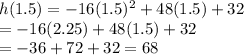
C) In this case we need to know when the function is 0. For this we can use the quadratic formula, with
![a=-16,\ b=48,\ c=32[\tex] and taking the positive solution.</p><p></p><p><strong>[tex]x_(1,2)=(-b\pm √(b^2-4ac))/(2a) = (-(48) \pm √(b(48)^2-4(-16)(32)))/(2(-16)) = (-48\pm √(2304+2048))/(-32)\\\\=(-48+√(4352))/(-32)\approx 3.56](https://img.qammunity.org/2020/formulas/mathematics/high-school/w47pvfcrk7l1frhha5eg2p1lfl5tc2r5sh.png)