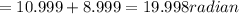Answer:
Total angular displacement will be 19.998 radian
Step-by-step explanation:
It is given that the washer starts from the rest and reach reach the speed of 2 rev/sec in 11 sec
So initial angular velocity
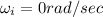
And final angular velocity
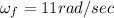
Time t = 11 sec
So angular acceleration
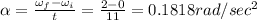
So angular displacement in this 11 sec
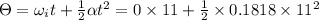
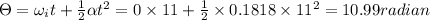
Now the washer slows down and stops in 9 sec
So final angular velocity = 0 rad/sec
So angular acceleration
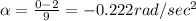
So angular displacement
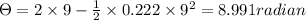
So total displacement in 20 sec =