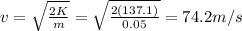Question

A 0.0500-kg golf ball heads off from the tee with an initial speed of 78.2 m/s and reaches to its maximum height of 37.8 m. If air resistance is neglected, (a) What is the kinetic energy of the ball at the pinnacle of its trajectory? (b) What is its speed when it is 5.60 m below the pinnacle point?

Answer 1

(a) 134.4 J

The total mechanical energy of the ball at the moment of launch is just equal to its initial kinetic energy:

`E=K_i = (1)/(2)mu^2`

where

m = 0.05 kg is the mass of the ball

u = 78.2 m/s is the initial speed

Substituting,

`E=(1)/(2)(0.05)(78.2)^2=152.9 J`

At the pinnacle of its trajectory, the total mechanical energy is sum of kinetic energy and potential energy:

`E=K_f + U_f = K_f + mgh`

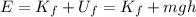
where

`g=9.8 m/s^2` is the acceleration of gravity

h = 37.8 m is the maximum height

Since the total energy must be conserved,

E = 152.9 J

Therefore, we can solve to find the kinetic energy of the ball at the pinnacle:

`K_f = E-mgh=152.9-(0.05)(9.8)(37.8)=134.4 J`

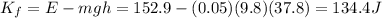
b) 74.2 m/s

When the ball is 5.60 m below the pinnacle point, the heigth of the ball is

`h=37.8-5.6=32.2 m`

So its potential energy is

`U=mgh=(0.05)(9.8)(32.2)=15.8 J`

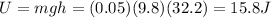
The total energy is again the sum of potential and kinetic energy:

E = K + U

So the kinetic energy at that point is

`K=E-U=152.9-15.8=137.1 J`

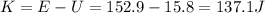
And since the kinetic energy is

`K=(1)/(2)mv^2`

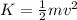
We can find the speed:

`v=\sqrt{(2K)/(m)}=\sqrt{(2(137.1))/(0.05)}=74.2 m/s`