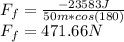Question

A 1500 kg car begins sliding down a 5.0o inclined road with a speed of 30 km/h. The engine is turned off, and the only forces acting on the car are a net frictional force from the road and the gravitational force. After the car has traveled 50 m along the road, its speed is 40 km/h.

(a) How much is the mechanical energy of the car reduced because of the net frictional force?
(b) What is the magnitude of that net frictional force?

Answer 1

a) -23583J

b) 471.66N

Step-by-step explanation:

Using the conservation energy theorem:

`K_o+U_o+W_f=K_f+U_f\\W_f=K_f+U_f-(K_o+U_o)`

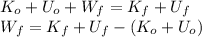
The height is given by:

`sin(\theta)=(h)/(d)\\\\h=50*sin(5^o)\\h=4.36m`

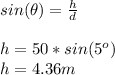
substituting the values we have:

`W_f=(1)/(2)*1500kg*((40-30)(km)/(h)*(1000h.m)/(3600km.s))^2+0-1500kg*9.8m/s^2*4.36m\\W_f=-23583J`*

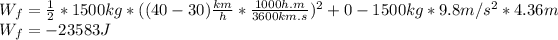the work is defined by:

`W_f=F_f*d*cos(\theta)`

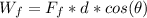
the force of the friction force is 180 degrees because it's opposite to the movement, so:

`F_f=(-23583J)/(50m*cos(180))\\F_f=471.66N`