Question

Bryce, a mouse lover, keeps his four pet mice in a roomy cage, where they spend much of their spare time (when they are not sleeping or eating) joyfully scampering about on the cage's floor. Bryce tracks his mice's health diligently and just now recorded their masses as 22.3 g, 17.9 g, 19.1 g, and 10.1 g. At this very instant, the x ‑ and y ‑components of the mice's velocities are, respectively, (0.349 m/s, −0.301 m/s), (−0.699 m/s, −0.815 m/s), (0.745 m/s, 0.975 m/s), and (−0.905 m/s, 0.717 m/s). Calculate the x ‑ and y ‑components of Bryce's mice's total momentum, px and py.

Answer 1

I₁ = (7.78 i ^ - 6.71 j ^) 10⁻³ J s , I₂ = (-12.5 i ^ -14.6 j ^) 10⁻³ J s , I₃ = (19.1i ^ + 18.6 j ^) 10⁻³ J s and I₄ = (-9.14i ^ + 7.24 j ^) 10⁻³ J s

Step-by-step explanation:

The impulse is equal to the variation of the moment, to apply this relationship to our case, we will assume that initially the mouse was at rest

I = Δp = m
`v_(f)` -m v₀

I = m (
`v_(f)` -v₀)

Bold indicates vector quantities, let's calculate the momentum of each mouse in for the x and y axes

We recommend bringing all units to the SI system

Mouse 1.

It has a mass of 22.3 g = 22.3 10⁻³ kg, a final velocity of (v = 0.349 i ^ - 0.301 j ^) m / s with an initial velocity of zero

Iₓ = m (
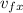`v_(fx)` - v₀ₓ)

Iₓ = 22.3 10⁻³ (0.349 -0)

Iₓ = 7.78 10⁻³ J s

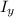`I_(y)` = m (
`v_(fy)` -
`v_(oy)` )

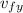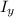`I_(y)` = 22.3 10⁻³ (-0.301)

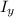`I_(y)` = -6.71 10⁻³ J s

I₁ = (7.78 i ^ - 6.71 j ^) 10⁻³ J s

Mouse 2

Mass 17.9 g = 17.9 10⁻³ kg

Speed ​​(-0.699 i ^ - 0.815 j ^) m / s

Iₓ = m (
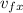`v_(fx)` - v₀ₓ)

Iₓ = 17.9 10⁻³ (-0.699 -0)

Iₓ = -12.5 10⁻³ J s

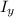`I_(y)` = 17.9 10⁻³ (-0.815 - 0)

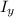`I_(y)` = -14.6 10⁻³ J s

I₂ = (-12.5 i ^ -14.6 j ^) 10⁻³ J s

Mouse 3

Mass 19.1 g = 19.1 10⁻³ kg

Speed ​​(0.745i ^ + 0.975 j ^) m / s

Iₓ = 19.1 10⁻³ (0.745 -0)

Iₓ = 14.2 10⁻³ J s

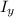`I_(y)` = 19.1 10⁻³(0.975 -0)

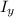`I_(y)` = 18.6 10⁻³ J s

I₃ = (19.1i ^ + 18.6 j ^) 10⁻³ J s

Mouse 4

Mass 10.1 g = 10.1 10⁻³ kg

Speed ​​(-0.905i ^ + 0.717j ^) m / s

Iₓ = 10.1 10⁻³ (-0.905 -0)

Iₓ = -9.14 10⁻³ J s

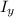`I_(y)` = 10.1 10⁻³ (0.717 -0)

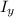`I_(y)` = 7.24 10⁻³ J s

I₄ = (-9.14i ^ + 7.24 j ^) 10⁻³ J s