Question

web based software company is interested in estimating the proportion of individuals who use the Firefox browser. In a sample of 200 of individuals, 30 users stated that they used Firefox. Using this data, construct a 99% confidence interval for the proportion of all individuals that use Firefox. What is the lower limit on the 99% confidence interval? Give your answer to three decimal places.

Answer 1

Answer with explanation:

Let
`\hat{p}` denotes the sample proportion.

As per given , we have

n= 200

`\hat{p}=(30)/(200)=0.15`

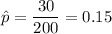
Critical value for 99% confidence :
`z_(\alpha/2)=2.576`

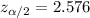
Confidence interval for population proportion :-

`\hat{p}\pm z_(\alpha/2) \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\\\\=0.15\pm (2.576)(\sqrt{(0.15(1-0.15))/(200)})\\\\\approx0.15\pm0.065\\\\=(0.15-0.065,\ 0.15+0.065)\\\\=(0.085,\ 0.215)`

Hence, a 99% confidence interval for the proportion of all individuals that use Firefox:
`(0.085,\ 0.215)`

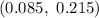
The lower limit on the 99% confidence interval = 0.085