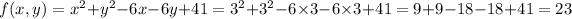Question

f(x,y)=x^2+y^2-6x-6y+41. How many critical points does g have in R22. If there is a local minimum, what is the value of the discriminant D at that point?3. If there is a local maximum, what is the value of the discriminant D at that point?4. If there is a saddle point, what is the value of the discriminant D at that point?5. What is the maximum value of f in R2?6. What is the minimum value of f in R2?

Answer 1

1) There is only a critical point at (3,3).

2) If there is a local minimum, the value of the discriminant must be D>0

3) If there is a local maximum, the value of the discriminant must be D>0

4) If there is a saddle point, the value of the discriminant must be D<0

5) There is not a local maximum of f

6) There is a local minimum at (3,3). f(3,3)=23

Explanation:

We have the fuction:

`f(x,y)=x^2+y^2-6x-6y+41`

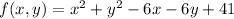
Its partial derivatives are:

`f_x=2x-6`

`f_y=2y-6`

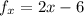
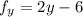
When
`f_x=0`

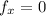
0=2x-6 ⇒ 2x=6 ⇒x=3

When
`f_y=0`

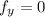
0=2y-6 ⇒ 2y=6 ⇒y=3

The critical point is (3,3)

Its second order derivatives are:

`f_(xx)=2`

`f_(yy)=2`

`f_(xy)=0`

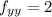
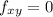
The value of the discriminant is

`D=f_(xx) * f_(yy)-(f_(xy))^2`=2×2-0=4

As D>0 and
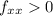`f_(xx)>0`, there is a local minimun at (3,3)

The value of f(x,y) at (3,3) is:

`f(x,y)=x^2+y^2-6x-6y+41=3^2+3^2-6*3-6*3+41=9+9-18-18+41=23`