Question

If one of the masses of the Atwood's machine below is 2.9 kg, what should be the other mass so that the displacement of either mass during the first second following release is 0.28 m? Assume a massless, frictionless pulley and a massless string. (There are two possible answers for m2. Enter your answers from smallest to largest.)

Answer 1

2.59 Kg, 3.25 Kg

Step-by-step explanation:

Acceleration can be found using equation

`s=0.5at^(2)` where s is the release distance, a is acceleration and t is time

Making a the subject of the formula

`a=\frac {2S}{t^(2)}`

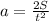
Substituting 0.28 for s and time for 1 second

Acceleration formula for the Atwood machine is given by

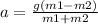`a=\frac {g(m1-m2)}{m1+m2}` where m1 and m2 are first and second masses respectively

Two situations are possible

When m1>m2

Assuming m1 is 3.7kg which is heavier than m2

Substituting a for
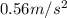`0.56 m/s^(2)` and m1 as 2.9Kg and taking acceleration due to gravity as
`9.81 m/s^(2)`

`0.56 m/s^(2)=\frac {9.81 m/s^(2)*(2.9Kg-m2)}{2.9Kg+m2}`

`(0.56 m/s^(2))*(2.9Kg+m2)=9.81(2.9Kg-m2)`

`(0.56 m/s^(2)+9.81)*m2=(9.81*2.9)-(2.9*0.56)`

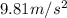
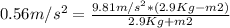
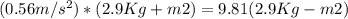
10.37m2=28.449-1.624

10.37m2=26.825

`m2=\frac {26.825}{10.37}=2.5867888138`

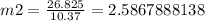
m2=2.59 Kg

When m1<m2

`a=\frac {g(m2-m1)}{m1+m2}`

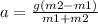
Then m1=2.9Kg hence

`0.56 m/s^(2)=\frac {9.81(m2-2.9Kg)}{2.9Kg+m2}`

`(0.56 m/s^(2))*(2.9Kg+m2)=9.81 m/s^(2)*(m2-2.9Kg)`

`(0.56 m/s^(2)-9.81 m/s^(2))*m2=(-2.9 Kg*9.81 m/s^(2))-(2.9 Kg*0.56 m/s^(2))`

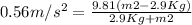
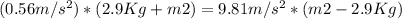
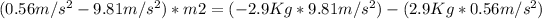
-9.25m2=-28.449-1.624=-30.073

9.25m2=30.073

`m2=\frac {30.073}{9.25}=3.2511351351`

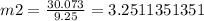
m2=3.25 Kg