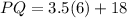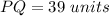Question

Given that PS is the perpendicular bisector of QR, PQ=3.5m+18, and PR=6m+3, identify PQ.

Answer 1

39

Explanation:

Triangles PQS and PRS are congruent

PQ = PR

3.5m + 18 = 6m + 3

2.5m = 15

m = 6

PQ = 3.5(6) + 18

PQ = 39

Answer 2

`PQ=39\ units`

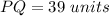
Explanation:

we know that

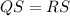`QS=RS` ----> equation A

Applying Pythagoras Theorem

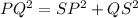`PQ^2=SP^2+QS^2` -----> equation B

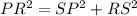`PR^2=SP^2+RS^2`-----> equation C

substitute equation A in equation C

`PR^2=SP^2+QS^2`

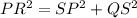
we have that

`PR^2=PQ^2`

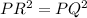
so

`PR=PQ`

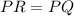
substitute the given values

`6m+3=3.5m+18`

Solve for m

`6m-3.5m=18-3`

`2.5m=15`

`m=6`

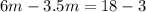
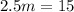
Find the value of PQ

`PQ=3.5m+18`

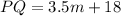
substitute the value of m

`PQ=3.5(6)+18`

`PQ=39\ units`