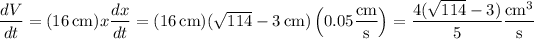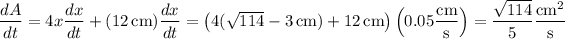Question

Please help meeeee math​

Answer 1

Q2. By the chain rule,

`(dy)/(dx) = (dy)/(dt) \cdot (dt)/(dx) = ((dy)/(dt))/((dx)/(dt))`

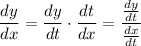
We have

`x=2t \implies (dx)/(dt)=2`

`y=t^4+1 \implies (dy)/(dt)=4t^3`

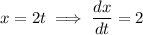
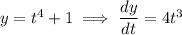
The slope of the tangent line to the curve at
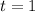`t=1` is then

`(dy)/(dx) \bigg|_(t=1) = (4t^3)/(2) \bigg|_(t=1) = 2t^3\bigg|_(t=1) = 2`

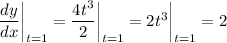
so the slope of the normal line is
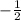`-\frac12`. When
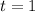`t=1`, we have

`x\bigg|_(t=1) = 2t\bigg|_(t=1) = 2`

`y\bigg|_(t=1) = (t^4+1)\bigg|_(t=1) = 2`

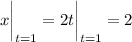
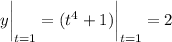
so the curve passes through (2, 2). Using the point-slope formula for a line, the equation of the normal line is

`y - 2 = -\frac12 (x - 2) \implies y = -\frac12 x + 3`

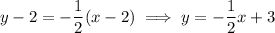
Q3. Differentiating with the product, power, and chain rules, we have

`y = x(x+1)^(1/2) \implies (dy)/(dx) = (3x+2)/(2√(x+1)) \implies (dy)/(dx)\bigg|_(x=3) = \frac{11}4`

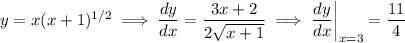
The derivative vanishes when

`(3x+2)/(2√(x+1)) = 0 \implies 3x+2=0 \implies x = -\frac23`

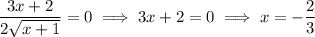
Q4. Differentiating with the product and chain rules, we have

`y = (2x+1)e^(-2x) \implies (dy)/(dx) = -4xe^(-2x)`

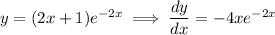
The stationary points occur where the derivative is zero.

`-4xe^(-2x) = 0 \implies x = 0`

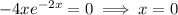
at which point we have

`y = (2x+1)e^(-2x) \bigg|_(x=0) = 1`

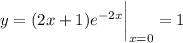
so the stationary point has coordinates (0, 1). By its "nature", I assume the question is asking what kind of local extremum this point. Compute the second derivative and evaluate it at
`x=0`.

`(d^2y)/(dx^2)\bigg|_(x=0) = (8x-4)e^(-2x)\bigg|_(x=0) = -4 < 0`

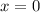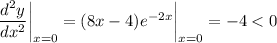
The negative sign tells us this stationary point is a local maximum.

Q5. Differentiating the volume equation implicitly with respect to
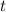`t`, we have

`V = \frac{4\pi}3 r^3 \implies (dV)/(dt) = 4\pi r^2 (dr)/(dt)`

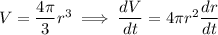
When
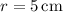`r=5\,\rm cm`, and given it changes at a rate
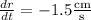`(dr)/(dt)=-1.5(\rm cm)/(\rm s)`, we have

`(dV)/(dt) = 4\pi (5\,\mathrm{cm})^2 \left(-1.5(\rm cm)/(\rm s)\right) = -150\pi (\rm cm^3)/(\rm s)`

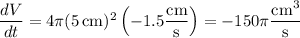
Q6. Given that
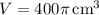`V=400\pi\,\rm cm^3` is fixed, we have

`V = \pi r^2h \implies h = (400\pi)/(\pi r^2) = (400)/(r^2)`

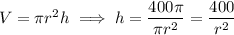
Substitute this into the area equation to make it dependent only on
`r`.

`A = \pi r^2 + 2\pi r \left((400)/(r^2)\right) = \pi r^2 + \frac{800\pi}r`

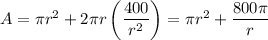
Find the critical points of
`A`.

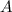`(dA)/(dr) = 2\pi r - (800\pi)/(r^2) = 0 \implies r = (400)/(r^2) \implies r^3 = 400 \implies r = 2\sqrt[3]{50}`

Check the sign of the second derivative at this radius to confirm it's a local minimum (sign should be positive).

`(d^2A)/(dr^2)\bigg|_{r=2\sqrt[3]{50}} = \left(2\pi + (1600\pi)/(r^3)\right)\bigg|_{r=2\sqrt[3]{50}} = 6\pi > 0`

Hence the minimum surface area is

`A\bigg_{r=2\sqrt[3]{50}\,\rm cm} = \left(\pi r^2 + \frac{800\pi}r\right)\bigg|_{r=2\sqrt[3]{50}\,\rm cm} = 60\pi\sqrt[3]{20}\,\rm cm^2`

Q7. The volume of the box is

`V = 8x^2`

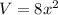
(note that the coefficient 8 is measured in cm) while its surface area is

`A = 2x^2 + 12x`

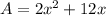
(there are two
`x`-by-
`x` faces and four 8-by-
`x` faces; again, the coefficient 12 has units of cm).

When
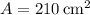`A = 210\,\rm cm^2`, we have

`210 = 2x^2 + 12x \implies x^2 + 6x - 105 = 0 \implies x = -3 \pm√(114)`

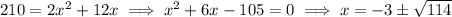
This has to be a positive length, so we have
`x=√(114)-3\,\rm cm`.

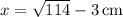Given that
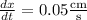`(dx)/(dt)=0.05(\rm cm)/(\rm s)`, differentiate the volume and surface area equations with respect to
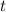`t`.

`(dV)/(dt) = (16\,\mathrm{cm})x (dx)/(dt) = (16\,\mathrm{cm})(√(114)-3\,\mathrm{cm})\left(0.05(\rm cm)/(\rm s)\right) = \frac{4(√(114)-3)}5 (\rm cm^3)/(\rm s)`

`(dA)/(dt) = 4x(dx)/(dt) + (12\,\mathrm{cm})(dx)/(dt) = \left(4(√(114)-3\,\mathrm {cm}) + 12\,\mathrm{cm}\right)\left(0.05(\rm cm)/(\rm s)\right) = \frac{√(114)}5 (\rm cm^2)/(\rm s)`