Question

Write an equation for the nth term of
the arithmetic sequence:
15,28,41 ....

Answer 1

The equation for the nth term of the given arithmetic sequence is:
`\mathbf{a_n=13n+22}`

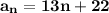
Explanation:

We need to write an equation for the nth term of the arithmetic sequence:

15,28,41 ....

The equation for arithmetic sequence is:
`a_n=a_1+(n-1)d`

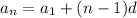
Where
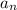`a_n` is the nth term,
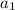`a_1` is first term and d is common difference

In the given sequence we have:

a₁ = 15

a₂ = 28

We can find common difference using the formula:

`a_n=a_1+(n-1)d\\Put\: n=2, a_2=28\: and\: a_1=15\\a_2=a_1+(2-1)d\\28=15+d\\d=28-15\\d=13`

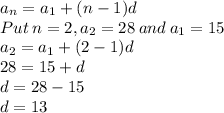
So, the common difference d is 13

Now, equation for nth term will be:

`a_n=a_1+(n-1)d\\Put\:a_1=15, d=13\\a_n=15+(n-1)13\\Solving:\\a_n=15+13n-13\\a_n=13n+2`

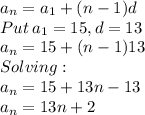
So, the equation for the nth term of the given arithmetic sequence is:
`\mathbf{a_n=13n+22}`

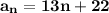
where n=1,2,3..