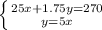Answer:
Variables:
 → The number of hours the worker worked
→ The number of hours the worker worked
 → The number of shirts the worker made.
→ The number of shirts the worker made.
System fo equations:
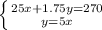
Explanation:
Let be
 the number of hours the worker worked and
the number of hours the worker worked and
 the number of shirts the worker made.
the number of shirts the worker made.
Since:
- Jason must pay the worker $25 per hour (which can be represented with
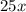 ).
). - He must pay $1.75 per shirt for material costs (which can be represented with
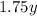 ).
). - The total expenses were $270.
You can write the following equation:

Knowing that the worker created an average of 5 shirts per hour, you can write the other equation:
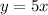
Therefore, with this equations you can set up the following system of equations, which could be used to determine the number of hours the worker worked and the number of shirts the worker made: