Answer:
The amount of the initial investment by Nina is $2271 approximately.
Solution:
Given, Nina invests a sum of money in a savings account with an annual interest rate of 4.61% compounded continuously.
After 6 years, the balance reaches $5274.56.
We have to find what was the amount of the initial investment?
We know that, compound interest is given as
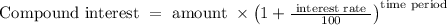
Now, balance = invested amount + compound interest.
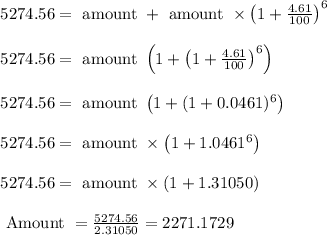
Hence, the invested amount of money is $2271 approximately.