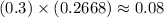Question

(1) In a bag of 10 donuts: every donut looks the same but 6 of them have the chocolate flavor and the other 4 have the vanilla flavor. Now you pick 3 donuts from these 10 donuts, what is the probability that you get 2 chocolate-flavor donuts and one vanilla-flavor donut? (2) A donut lover works in a donut factory and he works on a particular production line that produces chocolate-flavor and vanilla-flavor donuts. He hears from his boss that 30% of the donuts in that production line are chocolate-flavor ones. If one day, he will not resist so he will eat 10 donuts when he is working on that production line. What is the probability that he gets 5 chocolate-flavor donuts? (3) The same guy from question (2): If one day, he decides that he need to eat 4 chocolate-flavor donuts until he stops eating. So what is the probability that he eats 10 donuts that day?

Answer 1

a) 0.432, b) 0.1029 and c) 0.08

Explanation:

a) what is the probability that you get 2 chocolate-flavor donuts and one vanilla-flavor donut?

Observe that there are 3 possible ways for this to happen. Getting a vanilla donut first, second or third. And every of this cases has a probability of

`(6)/(10)* (6)/(10) * (4)/(10)=(144)/(1000)`

Therefore, the probability of a) to happen is given by:

`3* (144)/(1000)=(432)/(1000)=0.432`

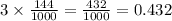
b) What is the probability that he gets 5 chocolate-flavor donuts?

Observe that:

• There are
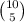  `{10 \choose 5}` ways to choose 5 chocolate donuts between 10
• The probability of each one of those cases to happen is given by
  `(0.3)^5*(0.7)^5`

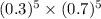
Therefore the probability of b) to happen is given by:

`{10\choose 5}*(0.3)^5*(0.7)^5=252*(0.00243)*(0.16807)\approx0.1029`

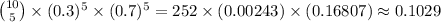
c) what is the probability that he eats 10 donuts that day?

Observe that, in order for the donut lover to eat exactly 10 donuts 2 things must happen

1. He should have eaten 9 donuts from which 3 of them were chocolate-flavored.
2. The 10th donut he ates must be a chocolate-flavored one.

Then we proceed to compute the probability of 1 the same way as in b).

• There are
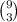  `{9 \choose 3}` ways to choose 3 chocolate donuts between 9
• The probability of each one of those cases to happen is given by
  `(0.3)^3*(0.7)^6`

Therefore the probability of 1 to happen is given by:

`{9\choose 3}*(0.3)^3*(0.7)^6=84*(0.027)*(0.117649)\approx0.2668`

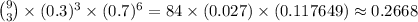
Finally the probability of 2 to happen is known to be 0.3 and, as 1 and 2 are independent events, the probability of both to happen is the multiplication of the probabilities. Then, the answer for c) is:

`(0.3)*(0.2668)\approx0.08`