Question

a ferris wheel is 35 meters in diameter, and can be boarded at ground level. The wheel turns in a counterclockwise direction, completing one full revolution every 5 minutes. Suppose that at t=0 you are in the three o'clock position. Find a possible formula

Answer 1

`y=17.5\sin\ \left((2\pi)/(5)x\right)+17.5`

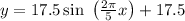
Explanation:

Diameter of a ferris wheel is 35 meters and it can be boarded at ground level.

It means,

Maximum value = 35

Minimum value = 0

The general sine function is

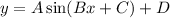`y=A\sin (Bx+C)+D` .... (1)

where, A is altitude,
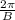`(2\pi)/(B)` is period, C/B is phase shift and D is midline.

The wheel turns in a counterclockwise direction, completing one full revolution every 5 minutes.

`Amplitude=A=(Maximum-Minimum)/(2)\Rightarrow (35-0)/(2)=17.5`

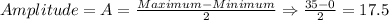
Period = 5

`5=(2\pi)/(B)`

`B=(2\pi)/(5)`

`Midline=D=(Maximum+Minimum)/(2)\Rightarrow (35+0)/(2)=17.5`

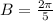
At t=0 you are in the three o'clock position. It means the graph passes through the point (0,17.5), which lies on the midline. So, the phase shift is 0.

Substitute A=17.5,
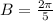`B=(2\pi)/(5)`, C=0 and D=17.5 in equation (1).

`y=17.5\sin\ \left((2\pi)/(5)x\right)+17.5`

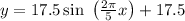
Therefore, the required formula is
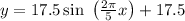`y=17.5\sin\ \left((2\pi)/(5)x\right)+17.5`.