Question

A team of astronauts is on a mission to land on and explore a large asteroid. In addition to collecting samples and performing experiments, one of their tasks is to demonstrate the concept of the escape speed by throwing rocks straight up at various initial speeds. With what minimum initial speed ????esc will the rocks need to be thrown in order for them never to "fall" back to the asteroid

Answer 1

v = √(2G M /
`r_(ast)`)

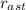Step-by-step explanation:

To find the escape velocity we can use the concept of conservation of mechanical energy, where we take at two points one on the surface of the asteroid and another distant point

Initial

Em₀ = K = ½ mv² - G m M /
`r_(ast)`

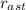
Final

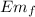`{Em}_(f)` = U = - G m M /
`r_(max)`

Where G is the universal gravitation constant value of 6.67 10⁻¹¹ Nm²/kg², M the mass of the asteroid and r is the distance from the stone to the asteroid

Em₀ =
`{Em}_(f)`

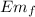
½ mv² - G m M /
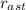`r_(ast)` = - G m M /
`r_(max)`

let's solve

½ v² = G M (1 /
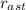`r_(ast)` -1 /
`r_(max)` )

The maximum distance value can be made infinite, so the last term becomes zero, so the escape velocity is

v = √(2G M /
`r_(ast)`)

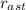where we assume that we know the mass and radius of the asteroid