Answer:
The specific gravity of the unkown liquid is 15.
Step-by-step explanation:
Gauge pressure, at the bottom of the tank in this case, can be calculated from
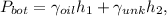
where
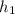 and
and
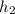 are the height of the column of oil and the unkown liquid, respectively. Writing for
are the height of the column of oil and the unkown liquid, respectively. Writing for
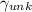 , we have
, we have
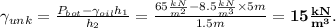
Relative to water, the unknow liquid specific weight is 15 times bigger, therefore this is its specific gravity as well.