Question

A survey conducted by the American Automobile Association showed that a family of four spends an average of $215.60 per day while on vacation. Suppose a sample of 64 families of four vacationing at Niagara Falls resulted in a sample mean of $252.45 per day and a sample standard deviation of $74.50.

a. Develop a 95% confidence interval estimate of the mean amount spent per day by a family of four visiting Niagara Falls.
b. Based on the confidence interval from part (a), does it appear that the population mean amount spent per day by families visiting Niagara Falls differs from the mean reported by the American Automobile Association? Explain.

Answer 1

A 95% confidence interval for the mean amount spent per day by a family of four visiting Niagara Falls is calculated to be approximately $234.20 to $270.70. Since this range does not include the AAA's reported mean of $215.60, it suggests that the population mean might be different from that reported by the AAA.

Step-by-step explanation:

To develop a 95% confidence interval estimate of the mean amount spent per day by a family of four vacationing at Niagara Falls, we will use the given sample mean, sample standard deviation, and the size of the sample along with the z-score associated with a 95% confidence level since the population standard deviation is unknown and the sample size is sufficiently large (n ≥ 30).

The formula to calculate the confidence interval is:

Confidence Interval = Sample Mean ± (z * (Sample Standard Deviation / sqrt(Sample Size)))

For a 95% confidence level, the z-score is approximately 1.96. Using the provided data of a sample mean of $252.45, a sample standard deviation of $74.50, and a sample size of 64 families, the calculations are:

Margin of Error = z * (Sample Standard Deviation / sqrt(Sample Size)) = 1.96 * ($74.50 / sqrt(64))

Margin of Error = 1.96 * ($74.50 / 8) = 1.96 * $9.3125 ≈ $18.25

The confidence interval is then:

$252.45 ± $18.25 = ($234.20, $270.70)

Regarding part (b), the confidence interval calculated in part (a) ranges from approximately $234.20 to $270.70. Since the interval does not include the mean reported by the American Automobile Association, which is $215.60, it appears that the population mean amount spent per day by families visiting Niagara Falls may differ from the mean reported by the AAA.

Answer 2

a) The 95% confidence interval estimate of the mean amount spent per day by a family of four visiting Niagara Falls is ($103.58, $401.32).

b) The population mean is inside the 95% confidence interval of the mean. So, it does not appear that the population mean amount spent per day by families visiting Niagara Falls differs from the mean reported by the American Automobile Association.

Step-by-step explanation:

The first step to solve this problem is solving question a), that is, building the confidence interval. Then question b), if the average spent by the families is inside the confidence interval, it does not appear that the population mean amount spent per day by families visiting Niagara Falls differs from the mean reported by the American Automobile Association. Otherwise, it does

a. Develop a 95% confidence interval estimate of the mean amount spent per day by a family of four visiting Niagara Falls.

The sample size is 64.

The first step to solve this problem is finding how many degrees of freedom there are, that is, the sample size subtracted by 1. So

`df = 64-1 = 63`

Then, we need to subtract one by the confidence level
`\alpha` and divide by 2. So:

`(1-0.95)/(2) = (0.05)/(2) = 0.025`

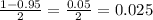
Now, we need our answers from both steps above to find a value T in the t-distribution table. So, with 63 and 0.025 in the t-distribution table, we have
`T = 1.9983`.

Now, we use the standard deviation of the sample. That is
`s = 74.50`

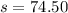
Now, we multiply T and s

`M = T*s = 74.50*1.9983 = 148.87`

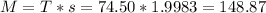
For the lower end of the interval, we subtract the mean by M. So 252.45 - 148.87 = $103.58.

For the upper end of the interval, we add the mean to M. So 252.45 + 148.87 = $401.32.

The 95% confidence interval estimate of the mean amount spent per day by a family of four visiting Niagara Falls is ($103.58, $401.32).

b. Based on the confidence interval from part (a), does it appear that the population mean amount spent per day by families visiting Niagara Falls differs from the mean reported by the American Automobile Association?

The population mean is inside the 95% confidence interval of the mean. So, yes, it does not appear that the population mean amount spent per day by families visiting Niagara Falls differs from the mean reported by the American Automobile Association.