Question

Speeding: On a stretch of Interstate-89, car speed is a normally distributed variable with a mean of 69.1 mph and a standard deviation of 3.3 mph. You are traveling at 73 mph. Approximately what percentage of cars are traveling faster than you? Enter your answer as a percentage with 1 decimal place.

Answer 1

Answer: 11.9%

Explanation:

Given : On a stretch of Interstate-89, car speed is a normally distributed variable with
`\mu=69.1` mph and
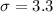`\sigma=3.3` mph.

Let x be a random variable that represents the car speed.

Since ,
`z=(x-\mu)/(\sigma)`

z-score corresponds x = 73 ,
`z=(73-69.1)/(3.3)\approx1.18`

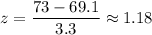
Required probability :

`\text{P-value }: P(x>73)=P(z>1.18)\\\\=1-P(z<1.18)\\\\1-0.8809999\\\\=0.1190001=11.90001\approx11.9\%`

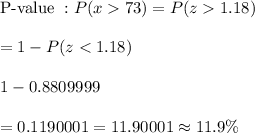
[using z-value table.]

Hence, the approximate percentage of cars are traveling faster than you = 11.9%