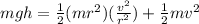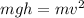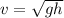Question

Consider the following objects of mass m rolling down an incline of height h. (a) A hoop has a moment of inertia I = mr2. What is the equation for the velocity vhoop of the hoop at the bottom of the incline? (Use the following as necessary: m, h, r, and g.)

Answer 1

`v = √(gh)`

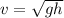
Step-by-step explanation:

As we know that when hoop is performing pure rolling on the inclined plane then work done by friction force on it must be zero

so we can use energy conservation for the two positions of the hoop

so here we have

initial potential energy of the hoop = final kinetic energy of the hoop

`mgh = (1)/(2)I\omega^2 + (1)/(2)mv^2`

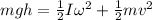
so we will have

`mgh = (1)/(2)(mr^2)((v^2)/(r^2)) + (1)/(2)mv^2`

`mgh = mv^2`

`v = √(gh)`