Question

The deflection plates in an oscilloscope are 10 cm by 2 cm with a gap distance of 1 mm. A 100 volt potential difference is suddenly applied to the initially uncharged plates through a 1000 ohm resistor in series with the deflection plates. How long does it take for the potential difference between the deflection plates to reach 65 volts?

Answer 1

18.5 ns.

Step-by-step explanation:

In order to develop the problem we must first identify the capacitance that is found

on the oscilloscope, like this:

`c =\frac{A \epsilon_ {0}}{d}`

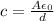
Where A scope of the oscilloscope,

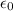`\epsilon_ {0}` is Vacuum permittivity

d = distance between the ones.

`C= (0.10m) (0.02m) (8.85 * 10 ^(- 12) C^ 2 / Nm ^ 2)/(1*10^(-3)m)`

`C = 17.7 * 10 ^(-12)F`

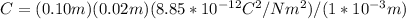
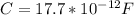
Defining the following variables in question we have to

Resistance (R) = 1000 Ohm

Meanwhile the Maximum Voltage (V_ {max}) applied is 100V

However, the maximum time to reach the voltage of 65V is

`V = V_ {max} (1- e ^(- t / (RC)))`

`65V = 100V (1-exp (-(t)/(1000 * 17.7 * 10^(-12)) )`

`0.65 = (1-exp (- (t)/(1000 * 17.7 * 10 ^( -12)))`

`ln (0.35) =-(t)/( 1000*17.7*10^(-12))`

`t = - 1000 * 17.7 * 10 ^ {- 12} ln (0.35)`

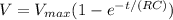
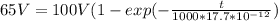
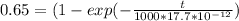
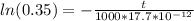
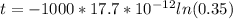
t = 18.5ns