Question

A tour operator has a bus that can accommodate 20 tourists. The operator knows that tourists may not show up, so he sells 21 tickets. The probability that an individual tourist will not show up is 0.02, independent of all other tourists. Each ticket costs 50, and is non-refundable if a tourist fails to show up. If a tourist shows up and a seat is not available, the tour operator has to pay 100 (ticket cost + 50 penalty) to the tourist. What is the expected revenue of the tour operator?

935
950
967
976
985

Answer 1

The expected revenue of the tour operator is 985.

Explanation:

There are two outcomes:

Either less than 21 tourists show up and the operator does not have to pay anything. Or 21 tourists show up and the operator has to repay 100.

Anyways, initially he gets the price of all the tickets sold. That is 21 each at 50, so
`R = 21*50 = 1050`.

Then, we need to find the probability that all of the 21 tourists show up. In this case, we have to subtract 100 from the revenue.

Each tourist has a 0.02 probability of not showing up. This means that each has a 1-0.02 = 0.98 probability of showing up. So the probability P that all 21 tourists show up is
`P = (0.98)^(21) = 0.6542`.

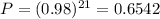So, the expected revenue of the tour operator is

`R = 1050 - 100P = 1050 - 100(0.6542) = 984.58`

Rounded up, the expected revenue of the tour operator is 985.