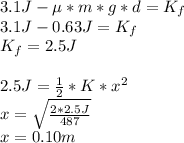Question

A block of mass m = 0.13 kg is set against a spring with a spring constant of k1 = 623 N/m which has been compressed by a distance of 0.1 m. Some distance in front of it, along a frictionless surface, is another spring with a spring constant of k2 = 487 N/m.(A) How far d2, in meters, will the second spring compress when the block runs into it?(B) How fast v, in meters per second, will the block be moving when it strikes the second spring?(C) Now assume friction is present on the surface in between the ends of the springs at their equilibrium lengths, and the coefficient of kinetic friction is ?k = 0.5. If the distance between the springs is x = 1 m, how far d2, in meters, will the second spring now compress?

Answer 1

a) 0.11 m

b) 6.9 m/s

c) 0.10 m

Step-by-step explanation:

We need to apply the conservation of energy theorem:

`U_e+K_(o)+U_o=K_f+U_f`

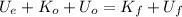
because the surface is frictionless all the elastic potential energy is converted in kinetic, so:

`(1)/(2)*k*x^2+0+0=K_f\\\\K_f=3.1J`

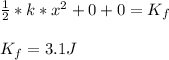
the second spring received 3.1J of energy, so:

`3.1J=(1)/(2)*487N/m*(x_2)^2\\x_2=0.11m`

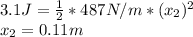
We know the value of the kinetic energy so:

`(1)/(2)m*(v_2)^2=3.1J\\v_2=\sqrt{(3.1J*2)/(0.13kg)}\\v_2=6.9m/s`

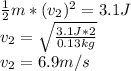
now if the surface has friction:

`3.1J-\µ*m*g*d=K_f\\3.1J-0.63J=K_f\\K_f=2.5J\\\\2.5J=(1)/(2)*K*x^2\\x=\sqrt{(2*2.5J)/(487)}\\x=0.10m`