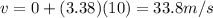Question

A 350 kg aircraft experiences a NET force of 1184 N at take off.

a) What’s is the aircraft’s acceleration?

b) Starting from rest, how fast will the aircraft be going after 10 seconds?

Answer 1

a)
`3.38 m/s^2`

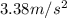
The acceleration of the aircraft can be found by using Newton's second law:

`F=ma`

where

F is the net force on the aircraft

m is the aircraft's mass

a is the acceleration

In this problem, we have

m = 350 kg

F = 1184 N

Re-arranging the equation for a, we find the acceleration of the plane:

`a=(F)/(m)=(1184)/(350)=3.38 m/s^2`

b) 33.8 m/s

Since the motion of the aircraft is a uniform accelerated motion, we can use the following suvat equation

`v=u+at`

where

v is the final velocity

u is the initial velocity

a is the acceleration

t is the time

For the aircraft in the problem,

u = 0 (it starts from rest)

`a=3.38 m/s^2` is the acceleration

Therefore, the velocity after t = 10 s is

`v=0+(3.38)(10)=33.8 m/s`