Question

A lecture hall at NC State has 220 seats with fold-down writing pedestals, 25 of which are designed for left-handers. An Intro. to Economics class with 215 students meets in this lecture hall. Assume that 13% of the general population is left-handed. Question 1. What is the probability that at least one right-handed student in this class is forced to use a seat designed for a left-hander? 0.01467 Incorrect: Your answer is incorrect. (Use 4 decimal places.) Question 2. What is the probability that at least one left-handed student in this class is forced to use a seat designed for a right-hander? 0.6648 Incorrect: Your answer is incorrect. (Use 3 decimal places.)

Answer 1

1) There is a 3.82% probability that at least one right-handed student in this class is forced to use a seat designed for a left-hander.

2) There is a 68.35% probability that at least one left-handed student in this class is forced to use a seat designed for a right-hander.

Explanation:

For each student, there are only two possible outcomes. Either they are right handed, or they are left handed. This means that we can solve this problem using binomial probability concepts.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).\pi^(x).(1-\pi)^(n-x)`

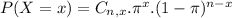
In which
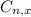`C_(n,x)` is the number of different combinatios of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

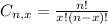
And
`\pi` is the probability of X happening.

In this problem, we have that:

13% of the students are left-handed and 100-13 = 87% are right handed.

There are 220 sets. Of them, 25 are designed for left handers and 220-25 = 195 for right handers.

There are 215 students, so
`n = 215`.

Question 1. What is the probability that at least one right-handed student in this class is forced to use a seat designed for a left-hander?

In this case, a success is a student being right-handed. So
`\pi = 0.87`.

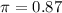There are 195 seats for right handed students. If there are 196 or more right handed students, they will have to use a seat designed for a left hander. We have to find
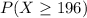`P(X \geq 196)`. Using a binomial probability calculator, we find that
`P(X \geq 196) = 0.0382`

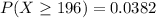
So, there is a 3.82% probability that at least one right-handed student in this class is forced to use a seat designed for a left-hander.

Question 2. What is the probability that at least one left-handed student in this class is forced to use a seat designed for a right-hander?

There are 25 seats for left-handed students. If there are 26, or more, at least one is going to be forced to use a seat designed for a right-hander.

In this case, a success is a student being left-handed. So
`\pi = 0.13`.

We have to find
`P(X \geq 26)`.

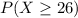Using a binomial probability calculator, we have that
`P(X \geq 26) = 0.6835`

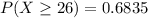
There is a 68.35% probability that at least one left-handed student in this class is forced to use a seat designed for a right-hander.