Answer:
-5.649065 and -0.942935
Explanation:
The degree of freedom will be given by
n - 1 where n is the sample number, given here as 15 so
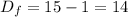
Critical time, t for a 95% confidence interval from the table is
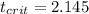
The 95% confidence levels will be given by
Limit=Parameter estimate ± Critical t * standard error of parameter estimate.
The standard error of parameter estimate is given as 1.097
First limit=-3.296 -( 2.145*1.097 )= -5.649065
Second limit = -3.296 + (2.145*1.097) = -0.942935