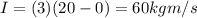1) 20 m/s
First of all, we can find the acceleration of the object using Newton's second law:

where
F = 20 N is the force applied
m = 3 kg is the mass of the object
a is the acceleration
Solving for a,
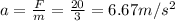
Now we can find the final velocity of the object using the suvat equation:

where
u = 0 is the initial velocity
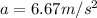 is the acceleration
is the acceleration
t = 3 s is the time
Substituting,
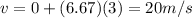
2) 60 kg m/s
The impulse exerted on the object is equal to its change in momentum:
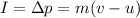
where
m is the mass
v is the final velocity
u is the initial velocity
For the object in the problem
m = 3 kg
u = 0
v = 20 m/s
Substituting,