Answer:
a.
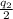
b. The optimal bundle is: 3 units of q1 and 2 units of q2.
c. If the income falls to 20, Jezz would have to consume 1 unit of one good and 0 of the other (corner solution). The MRS is equal to 1 and it is not possible to establish an equivalence with the MRT, since to calculate it we would need to know a production function, which does not appear anywhere in the problem statement.
Step-by-step explanation:
a. What is the marginal rate of substitution for this utility function?
Theoretically, the marginal rate of substitution (MRS) is defined as the number of units of a good to which a consumer is willing to give up in exchange for an additional unit of the other good, keeping the same level of utility.
To find it, we must follow this equation:
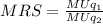
Where:
MUq1 = Marginal Utility of good 1.
MUq2 = Marginal Utility of good 2.
Therefore, we must find the marginal utilities of both goods. For good 1, we differentiate the utility function with respect to q1:
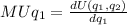

Here the result is 1, because what we derive q1, or otherwise seen: 1 * q1 raised to 1). Then, 1 (that is in the exponent) is multiplied by the number that accompanies the term, so 1 * 1 = 1, and q1 would be raised to 0, which is equivalent to 1.
For good 2, we differentiate the utility function with respect to q2:
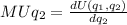
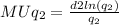

Once the marginal utility of each good is obtained, the marginal rate of substitution is found:
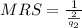
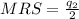
b. Solve for Jezz's optimal bundle.
In the first place, the budget line must be found, which is the set of different combinations of two goods that can be consumed by an individual from an income level and given certain prices for each good.
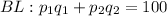
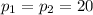
Therefore:
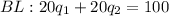
Now we must establish the condition that the optimal bundle should meet:
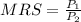
We replace the MRS obtained in the previous point and the prices:
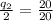
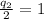

Now we substitute the value of q2 on the budget line, to find q1:
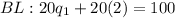
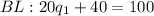


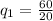

Therefore, the optimal amount of goods given the budget constraint is: 3 units of q1 and 2 units of q2.
c. Suppose Jezz's income falls to $20. What will happen to his optimal bundle? Is the MRS = MRT at the optimal bundle?
The previous procedure is repeated, but in this case the budget line equals 20.

Now we must establish the condition that the optimal bundle should meet:
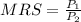
We replace the MRS obtained in the previous point and the prices:
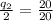
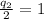

Now we substitute the value of q2 on the budget line, to find q1:
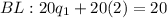

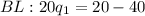
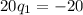
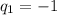
Certainly, no one can consume negative amounts of any good. This result can be interpreted as follows: Jezz's income would allow him to consume either a unit of q1 or a unit of q2, but always the consumption of either of the two goods must be 0. This is what is known as a corner solution, a situation in which the consumer is unable to make a tradeoff between two goods.
To find the MRS, we replace as follows:
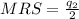

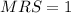
The MRS is 1, that means that in order to keep the level of utility constant, Jezz would be willing to give up one unit of some of the goods, in order to consume one unit of the other.
With the data of the statement it is not possible to find the Marginal Rate of Transformation, a concept homologous to that of MRS, but oriented to the supply side, which indicates the number of units of a good that must be forgone to create an additional unit of another good. To calculate it, it would be necessary to know a production function.