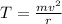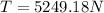Question

A string under a tension of 68 N is used to whirl a rock in a horizontal circle of radius 3.7 m at a speed of 16.53 m/s. The string is pulled in, and the speed of the rock increases. When the string is 0.896 m long and the speed of the rock is 71.5 m/s, the string breaks. What is the breaking strength of the string? Answer in units of N.

Answer 1

Answer:5249.18 N

Step-by-step explanation:

Given

When Tension T is 68 N velocity v=16.53 m/s

radius r=3.7 m

as the rock is in the horizontal position thus tension will provide the centripetal acceleration

`T=(mv^2)/(r)`

`68=(m* 16.53^2)/(3.7)`

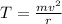
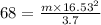
m=0.92 kg

when Velocity is 71.5 m/s and r=0.896 m string breaks

therefore breaking strength of string is

`T=(mv^2)/(r)`

`T=(0.92* 71.5^2)/(0.896)`

`T=5249.18 N`

Answer 2

`F = 5253.7 N`

Step-by-step explanation:

As we know that tension force in the string will be equal to the centripetal force on the string

so we will have

`T = (mv^2)/(L)`

now we have

`68 = (m(16.53^2))/(3.7)`

now we have

`68 = 73.8 m`

`m = 0.92 kg`

now when string length is 0.896 m and its speed is 71.5 m/s then we will have

`F = (mv^2)/(r)`

`F = (0.92(71.5^2))/(0.896)`

`F = 5253.7 N`