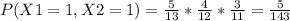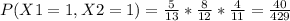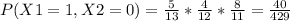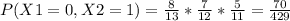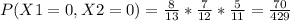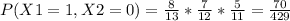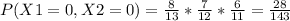Question

Suppose that 3 balls are chosen without replacement from an urn consisting of 5 white and 8 red balls. Let X i equal 1 if the i th ball selected is white, and let it equal 0 otherwise. Give the joint probability mass function of X 1 , X 2 ; X 1 , X 2 , X 3 .

Answer 1

Mixed probabilty

Explanation:

What is the probability that the first and second ball chosen are both targets, that is, X1 = 1 X2 = 2?

For this we must study the simple probability of each, for example for the target in that event is 5/13. However for the second chosen but also white in the second event where there is already a total of 12 balls is 4/12.

Thus

`P (X1 = 1, X2 = 1) = (5)/(13) * (4)/(12) = (5)/(39)`

In this way is generated for all probabilities

`P (X1 = 1, X2 = 0) = (5)/(13) *(8)/(12) = (10)/(39)\\P (X1 = 0, X2 = 1) = (8)/(13) * (5)/(12) = (10)/(39)\\P (X1 = 0, X2 = 0) = (8)/(13) *(7)/(12) =(4)/(39)\\`

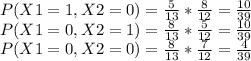
b) In the same way analogous to the past example we can perform all cases of combinations, therefore it would be so

`P (X1 = 1, X2 = 1) = (5)/(13)*(4)/(12)*(3)/(11)= (5)/(143)`

`P (X1 = 0, X2 = 1) = (8)/(13) *(5)/(12) * (4)/(11) = (40)/(429)`

`P (X1 = 1, X2 = 1) = (5)/(13)*(8)/(12)*(4)/(11) = (40)/(429)`

`P (X1 = 1, X2 = 0) =(5)/(13)*(4)/(12)*(8)/(11) = (40)/(429)`

`P(X1 = 0, X2 = 1) = (8)/(13)* (7)/(12)*(5)/(11)=(70)/(429)`

`P (X1 = 0, X2 = 0) = (8)/(13) * (7)/(12) * (5)/(11) = (70)/(429)`

`P (X1 = 1, X2 = 0) = (8)/(13) * (7)/(12) * (5)/(11) = (70)/(429)`

`P (X1 = 0, X2 = 0) = (8)/(13) *(7)/(12) * (6)/(11) = (28)/(143)`