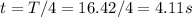Answer:
4.11 s.
Step-by-step explanation:
The period T of oscillation of the pendulum is given by the formula:
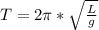
The maximum oscillation point it can reach is 45 °,
This point is the equivalent of T / 4, which is the moment when it reaches equilibrium.
So for T / 4,