Question

Franklin Corporation is comparing two different capital structures, an all-equity plan (Plan I) and a levered plan (Plan II). Under Plan I, the company would have 200,000 shares of stock outstanding. Under Plan II, there would be 150,000 shares of stock outstanding and $2.2 million in debt outstanding. The interest rate on the debt is 5 percent and there are no taxes.

a. If EBIT is $350,000, what is the EPS for each plan? (Do not round intermediate calculations and round your answers to 2 decimal places, e.g., 32.16.)

EPS
Plan I $
Plan II $

b. If EBIT is $600,000, what is the EPS for each plan? (Do not round intermediate calculations and round your answers to 2 decimal places, e.g., 32.16.)

EPS
Plan I $
Plan II $

c. What is the break-even EBIT? (Enter your answer in dollars, not millions of dollars, e.g., 1,234,567. Do not round intermediate calculations and round your answer to the nearest whole number, e.g., 32.)

Break-even EBIT $

Answer 1

a) unlevered: 1.75 EPS

levered: 1.60 EPS

b)unlevered: 3.00 EPS

levered: 3.27 EPS

c) EBIT break even point: 440,000 dollars

at this point is indifferent which plan the firm chose.

Step-by-step explanation:

unlevered firm:

200,000 shares (100%)

levered firm

150,000 shares (75%)

Debt: $2,200,000 (25%)

a) EBIT: 350,000

unlevered: 350,000/200,000 = 1.75 EPS

levered: (350,000-2,200,000x5%)/150,000 = 1.6 EPS

b) EBIT: 650,000

unlevered: 600,000/200,000 = 3 EPS

levered: (600,000-2,200,000x5%)/150,000 = 3.27 EPS

c) we should build and equation system at which both plans get the same EPS:

`\left \{ {{EPS_u=(EBIT)/(200,000) }\\ \atop {EPS_l=(EBIT-interest)/(150,000) }} \right.`

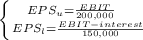
We equalize and solve for EBIT:

`(EBIT)/(200,000) = (EBIT-interest)/(150,000)`

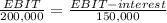
interest is: 2,200,000 x 5% = 110,000

`(EBIT)/(200,000) * 150,000 = EBIT-110,000`

`EBIT * 0.75 = EBIT-110,000`

`(1 - 0.75)EBIT = 110,000`

`EBIT = 110,000 / 0.25`

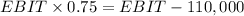
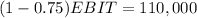
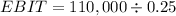
EBIT = 440,000