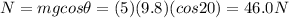Question

Write out newton's second law for the direction that is perpendicular to the ramp

The right triangles long side has a box sliding down with a mass of 5 kg and its a 20 degree ramp

Answer 1

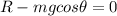`R-mg cos \theta = 0`, R = 46.0 N

Step-by-step explanation:

For an object on a ramp, there are two forces acting along the direction perpendicular to the ramp:

- The normal reaction of the surface, N, out of the ramp

- The component of the weight perpendicular to the ramp, in the opposite direction, of magnitude

`mg cos \theta`

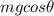
where

m is the mass of the block

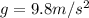`g=9.8 m/s^2` is the acceleration of gravity

`\theta` is the angle of the ramp

The box is in equilibrium along this direction, so the equation of the forces in this direction is

`R-mg cos \theta = 0`

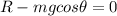
In this problem,

m = 5 kg

`\theta=20^(\circ)`

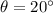
So we can find the normal reaction:

`N=mg cos \theta = (5)(9.8)(cos 20)=46.0 N`