Answer: 0.0082
Explanation:
Let x be the random variable that represents the opening altitude.
We assume that opening altitude actually has a normal distribution .
As per given , we have
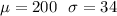
Equipment damage will occur if the parachute opens at an altitude of less than 100 m.
z-score corresponds to x=100,
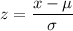
i.e.
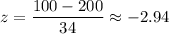
P-value =
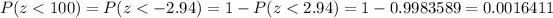
Let Y be a binomial variable that represents the opening altitude.
with parameters p=0.0016411 , n= 5
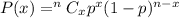
Required probability :
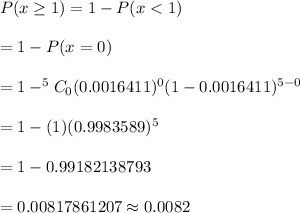
Hence, the probability that there is equipment damage to the payload of at least one of five independently dropped parachutes = 0.0082