Question

The side lengths of triangle a are increased by 40%. The side lengths of triangle b do not change. What is the new ratio of the area of triangle a to triangle b?

Answer 1

To find the new ratio of the area of triangle a to triangle b, compare the areas of the triangles before and after the side lengths of triangle a are increased by 40%.

Step-by-step explanation:

To find the new ratio of the area of triangle a to triangle b, we need to compare the areas of the triangles before and after the side lengths of triangle a are increased by 40%. Let's assume the original side lengths of triangle a were x, y, and z, and the side lengths of triangle b were p, q, and r.

The ratio of the areas of triangle a to triangle b before the increase in side lengths is proportional to (x*y*z) / (p*q*r).

After increasing the side lengths by 40%, the new side lengths of triangle a are 1.4x, 1.4y, and 1.4z. The ratio of the areas of triangle a to triangle b after the increase in side lengths is proportional to ((1.4x)*(1.4y)*(1.4z)) / (p*q*r).

Answer 2

1.96 : 1

Step-by-step explanation:

The area of a triangle is

`A=(1)/(2)bh`

Where b is the base and h is the height

Since triangle b's side do not change, let base be b and height be h, so area would simply be
`A=(1)/(2)bh`

Since side lengths are increased by 40%, that means:

40% = 40/100 = 0.4

Increase of this means "multiply by 1.4"

So base will increase by this as well as height. So with respect to triangle b, triangle a's area would be:

`A=(1)/(2)(1.4b)(1.4h)\\A=(1)/(2)(1.4*1.4)bh\\A=(1)/(2)bh*1.96`

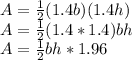
So, there's an extra factor of 1.96 which means area increased by 96%!

So, we find ratio of triangle a to triangle b (area) by dividing area of triangle a to triangle b:

`((1)/(2)bh(1.96))/((1)/(2)bh)\\=1.96:1`

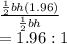
So the ratio is 1.96:1