Answer: 0.0250
Explanation:
Given : A statistics professor plans classes so carefully that the lengths of her classes are uniformly distributed between 50.0 and 60.0 minutes.
We know that the uniform distribution is also known as rectangular distribution.
Density function for uniform distribution :
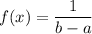
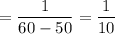
Now, the probability that a given class period runs between 51.25 and 51.5 minutes :-
![\int^(51.5)_(51.25)f(x)\ d(x)\\\\ \int^(51.5)_(51.25)(1)/(10)\ dx\\\\=(1)/(10) [x]^(51.5)_(51.25)\\\\=(1)/(10)(51.5-51.25)=0.0250](https://img.qammunity.org/2020/formulas/mathematics/high-school/1s0dwfl0v7miu10gq8kjflisapepu8wyv5.png)
Hence, the probability that a given class period runs between 51.25 and 51.5 minutes = 0.0250