Answer:
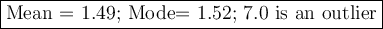
Explanation:
When sorted, your data are:
0.01, 0.01, 0.08, 0.14, 0.24, 0.35, 0.57, 0.64, 0.65, 0.67, 0.69, 0.74, 0.81
0.82, 0.92, 0.99, 1.01, 1.04, 1.15, 1.16, 1.33, 1.41, 1.45, 1.48, 1.52
1.53, 1.58, 1.61, 1.62, 1.73, 1.77, 1.78, 1.84, 1.98, 2.01, 2.02, 2.03, 2.06
2.06, 2.31, 2.41, 2.53, 2.55, 2.59, 2.66, 2.74, 2.74, 2.77, 2.77, 2.91
I entered the data into a statistical and box plot generator.
The results were:
mean = 1.49
Median = 1.52
Q1 = 0.81
Q2 = 1.525
Q3 = 2.06
IQR = 1.25
One test for an outlier is if the value is greater than the upper fence: Q3 + 1.5IQR.

The box-and-whisker plot shows that a value of 7.0 is well above the upper fence (in red).