Question

Having two roots y intercept -1 and with vertex (-1,22)

Answer 1

Vertex form: y = -23(x + 1)² + 22

Standard form: y = -23x² - 46x - 1

Roots at (-1.978, 0) and (-0.022, 0)

Explanation:

The vertex form of the equation for a parabola is

y = a(x - h)² + k

where h and k are the coordinates of the vertex and a is a constant.

Data:

Vertex at (-1,22)

y-intercept at (0, -1)

Calculations:

1. Substitute the coordinates of the vertex into the equation

y = a(x + 1)² + 22

2. Substitute the coordinates of the y-intercept into the equation and solve for a

`\begin{array}{rcl}y&=& a(x +1)^(2) + 22\\-1 & = & a(0 +1)^(2) + 22\\-1 & = & a(1)^(2) + 22\\-1 & = & a+ 22\\\mathbf{a} & = &\mathbf{-23}\\\end{array}`

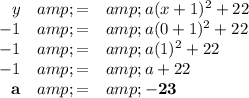
The equation of the parabola in vertex form is

y = -23(x + 1)² + 22

To convert the equation to standard form, you expand the vertex form.

`\begin{array}{rcl}y & = & -23(x + 1)^(2) + 22\\y & = & -23(x^(2) + 2x + 1) + 22\\y & = & -23x^(2) - 46x - 23 + 22\\\mathbf{y} & = &\mathbf{-23x^(2) - 46x - 1}\\\end{array}`

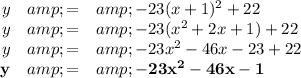
The equation of the parabola in standard form is

y = -23x² - 46x - 1

3. Find the roots

The roots are the values of x that make y = 0

`\begin{array}{rcl}0 & = & -23(x + 1)^(2) + 22\\23(x + 1)^(2)  & = & 22\\(x + 1)^(2)  & = & (22)/(23)\\\\x + 1 & = & \pm \sqrt{(22)/(23)}\\\\x & = & -1 \pm \sqrt{(22)/(23)}\\\\x = -1-\sqrt{(22)/(23)} && x = -1+\sqrt{(22)/(23)}\\\\x = -1-0.978 && x = -1+0.978\\\mathbf{x= -1.978} && \mathbf{x = -0.022}\\\end{array}`

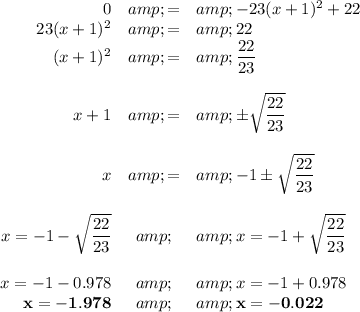
The roots are at x = -1.978 and x = -0.022.

The graph shows your parabola with vertex (-1, 22), y-intercept at (0, -1). and x-intercepts at (-1.978, 0) and (-0.022, 0).