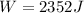Answer:
W = 2352 J
Step-by-step explanation:
Given that:
- mass of the bucket, M = 10 kg
- velocity of pulling the bucket, v = 3
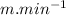
- height of the platform, h = 30 m
- rate of loss of water-mass, m =
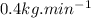
Here, according to the given situation the bucket moves at the rate,
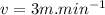
The mass varies with the time as,

Consider the time interval between t and t + ∆t. During this time the bucket moves a distance
∆x = 3∆t meters
So, during this interval change in work done,
∆W = m.g∆x
For work calculation:
![W=\int_(0)^(10) [(10-0.4t).g* 3] dt](https://img.qammunity.org/2020/formulas/physics/college/s92fzqh652iwnc1h0af4kg17qc0d8yqe3i.png)
![W= 3* 9.8* [10t-(0.4t^(2))/(2)]^(10)_(0)](https://img.qammunity.org/2020/formulas/physics/college/i7r3a25jvw3s7351ct2wtuysnjmw449whq.png)